Dưới đây là bài số 2 trong chuỗi bài hướng dẫn chi tiết về Sử dụng đẳng thức chứng minh bất đằng thức
Đẳng thức đáng nhớ 2
Với
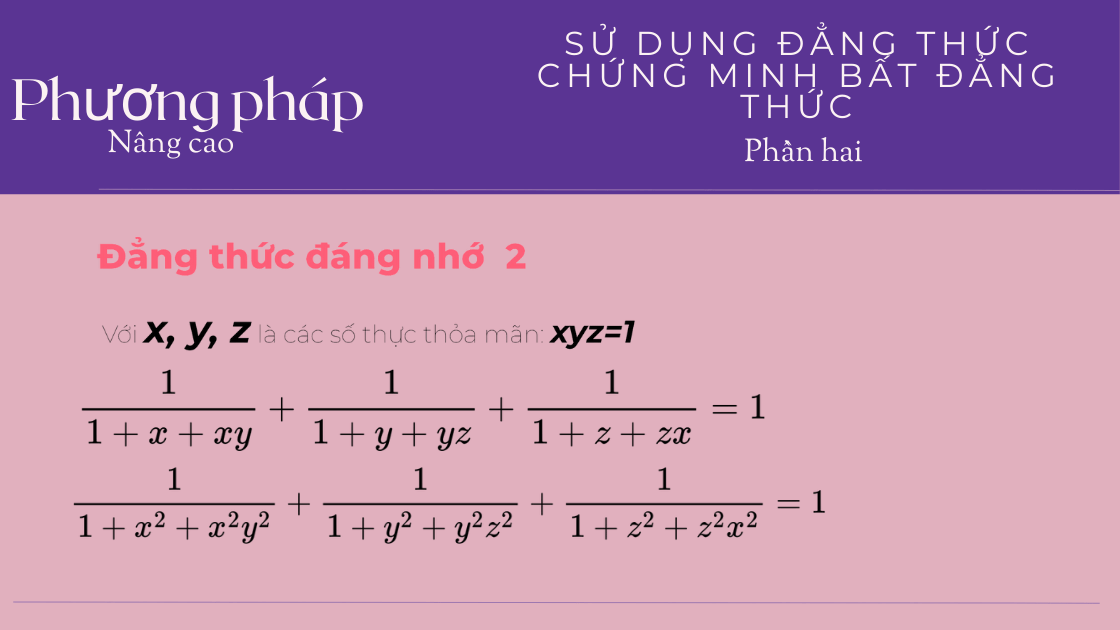
x , y , z x, y, z x , y , z là các số thực thỏa mãn:
x y z = 1 x y z=1 x yz = 1 Ta có các kết quả sau:
Kết quả 1. Đẳng thức:
1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x = 1 \frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}=1 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 = 1 Kết quả 2. Đẳng thức
1 1 + x 2 + x 2 y 2 + 1 1 + y 2 + y 2 z 2 + 1 1 + z 2 + z 2 x 2 = 1 \frac{1}{1+x^{2}+x^{2} y^{2}}+\frac{1}{1+y^{2}+y^{2} z^{2}}+\frac{1}{1+z^{2}+z^{2} x^{2}}=1 1 + x 2 + x 2 y 2 1 + 1 + y 2 + y 2 z 2 1 + 1 + z 2 + z 2 x 2 1 = 1 Chứng minh nên
1 1 + y + y z = x x + x y + x y z = x 1 + x + x y \frac{1}{1+y+y z}=\frac{x}{x+x y+x y z}=\frac{x}{1+x+x y} 1 + y + yz 1 = x + x y + x yz x = 1 + x + x y x v a ˋ 1 1 + z + z x = x y x y + x y z + x 2 y z = x y 1 + x + x y \text{và }\frac{1}{1+z+z x}=\frac{x y}{x y+x y z+x^{2} y z}=\frac{x y}{1+x+x y} v a ˋ 1 + z + z x 1 = x y + x yz + x 2 yz x y = 1 + x + x y x y
Do đó:
1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x = 1 1 + x + x y + x 1 + x + x y + x y 1 + x + x y = 1 \frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}=\\\frac{1}{1+x+x y}+\frac{x}{1+x+x y}+\frac{x y}{1+x+x y}=1 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 = 1 + x + x y 1 + 1 + x + x y x + 1 + x + x y x y = 1
Vậy đẳng thức được chứng minh.
Nhận xét: Từ đẳng trước trên có thể suy ra với các số thực x, y, z thỏa mãn xyz = 1
thì ta có:
1 1 + x 2 + x 2 y 2 + 1 1 + y 2 + y 2 z 2 + 1 1 + z 2 + z 2 x 2 = 1 \frac{1}{1+x^{2}+x^{2} y^{2}}+\frac{1}{1+y^{2}+y^{2} z^{2}}+\frac{1}{1+z^{2}+z^{2} x^{2}}=1 1 + x 2 + x 2 y 2 1 + 1 + y 2 + y 2 z 2 1 + 1 + z 2 + z 2 x 2 1 = 1 Ví dụ bài toán sử dụng Thí dụ 1. Cho ba số thực dương x, y, z thỏa mãn x y z=1. Chứng minh rằng:
1 2 x 2 + y 2 + 3 + 1 2 y 2 + z 2 + 3 + 1 2 z 2 + x 2 + 3 ≤ 1 2 \frac{1}{2 x^{2}+y^{2}+3}+\frac{1}{2 y^{2}+z^{2}+3}+\frac{1}{2 z^{2}+x^{2}+3} \leq \frac{1}{2} 2 x 2 + y 2 + 3 1 + 2 y 2 + z 2 + 3 1 + 2 z 2 + x 2 + 3 1 ≤ 2 1
Hướng dẫn giải Do bất đẳng thức đối xứng với x, y, z nên dễ đoán được đẳng thức xảy ra khi x=y=z=1
Sử dụng
bất đẳng thức AM-GM cho các số dương ta được:
2 x 2 + y 2 + 3 = ( x 2 + y 2 ) + ( x 2 + 1 ) + 2 ≥ 2 x y + 2 x + 2 2x^{2}+y^{2}+3=\left(x^{2}+y^{2}\right)+\left(x^{2}+1\right)+2 \geq 2 x y+2 x+2 2 x 2 + y 2 + 3 = ( x 2 + y 2 ) + ( x 2 + 1 ) + 2 ≥ 2 x y + 2 x + 2 ⇒ 1 2 x 2 + y 2 + 3 ≤ 1 2 ( 1 + x + x y ) \Rightarrow \frac{1}{2 x^{2}+y^{2}+3} \leq\frac{1}{2(1+x+x y)} ⇒ 2 x 2 + y 2 + 3 1 ≤ 2 ( 1 + x + x y ) 1
Chứng minh tương tự ta được:
$$
1 2 y 2 + z 2 + 3 ≤ 1 2 ( 1 + y + y z ) \frac{1}{2 y^{2}+z^{2}+3} \leq \frac{1}{2(1+y+y z)} 2 y 2 + z 2 + 3 1 ≤ 2 ( 1 + y + yz ) 1 1 2 z 2 + x 2 + 3 ≤ 1 2 ( 1 + x + z x ) \frac{1}{2 z^{2}+x^{2}+3} \leq \frac{1}{2(1+x+z x)} 2 z 2 + x 2 + 3 1 ≤ 2 ( 1 + x + z x ) 1
Cộng theo vế ba bất đẳng thức trên ta được:
1 2 x 2 + y 2 + 3 + 1 2 y 2 + z 2 + 3 + 1 2 z 2 + x 2 + 3 ≤ 1 2 ( 1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x ) \frac{1}{2 x^{2}+y^{2}+3}+\frac{1}{2y^{2}+z^{2}+3}+\frac{1}{2 z^{2}+x^{2}+3} \leq \frac{1}{2}\left(\frac{1}{1+x+xy}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}\right) 2 x 2 + y 2 + 3 1 + 2 y 2 + z 2 + 3 1 + 2 z 2 + x 2 + 3 1 ≤ 2 1 ( 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 )
Mà ta đã biết đẳng thức:
1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x = 1 \frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}=1 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 = 1 Vậy bài toán được chứng minh.
Đẳng thức xảy ra khi
x = y = z = 1 \mathrm{x}=\mathrm{y}=\mathrm{z}=1 x = y = z = 1 .
Thí dụ 2. Cho ba số thực dương x, y, z thỏa mãn x y z = 1 x y z=1 x yz = 1 Tìm giá trị lớn nhất của biểu thức:
C = 1 ( x + 1 ) 2 + y 2 + 1 + 1 ( y + 1 ) 2 + z 2 + 1 + 1 ( z + 1 ) 2 + x 2 + 1 C=\frac{1}{(x+1)^{2}+y^{2}+1}+\frac{1}{(y+1)^{2}+z^{2}+1}+\frac{1}{(z+1)^{2}+x^{2}+1} C = ( x + 1 ) 2 + y 2 + 1 1 + ( y + 1 ) 2 + z 2 + 1 1 + ( z + 1 ) 2 + x 2 + 1 1
Hướng dẫn giải
Do bất đẳng thức đối xứng với x, y, z nên dễ đoán được đẳng thức xảy ra khi x=y=z=1.
Sử dụng bất đẳng thức
AM - GM cho các số dương ta được:
( x + 1 ) 2 + y 2 + 1 = x 2 + y 2 + 2 x + 2 ≥ 2 x y + 2 x + 2 (x+1)^{2}+y^{2}+1=x^{2}+y^{2}+2 x+2 \geq 2 x y+2 x+2 ( x + 1 ) 2 + y 2 + 1 = x 2 + y 2 + 2 x + 2 ≥ 2 x y + 2 x + 2 ⇒ 1 ( x + 1 ) 2 + y 2 + 1 ≤ 1 2 ( x y + x + 1 ) \Rightarrow \frac{1}{(x+1)^{2}+y^{2}+1} \leq \frac{1}{2(x y+x+1)} ⇒ ( x + 1 ) 2 + y 2 + 1 1 ≤ 2 ( x y + x + 1 ) 1
Chứng minh tương tự ta được:
1 ( y + 1 ) 2 + z 2 + 1 ≤ 1 2 ( z y + y + 1 ) ; \frac{1}{(y+1)^{2}+z^{2}+1} \leq \frac{1}{2(z y+y+1)} ; ( y + 1 ) 2 + z 2 + 1 1 ≤ 2 ( zy + y + 1 ) 1 ; 1 ( z + 1 ) 2 + x 2 + 1 ≤ 1 2 ( z x + z + 1 ) \frac{1}{(z+1)^{2}+x^{2}+1} \leq \frac{1}{2(z x+z+1)} ( z + 1 ) 2 + x 2 + 1 1 ≤ 2 ( z x + z + 1 ) 1
Cộng theo vế ba bất đẳng thức trên ta được:
C = 1 ( x + 1 ) 2 + y 2 + 1 + 1 ( y + 1 ) 2 + z 2 + 1 + 1 ( z + 1 ) 2 + x 2 + 1 ≤ 1 2 ( 1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x ) C=\frac{1}{(x+1)^{2}+y^{2}+1}+\frac{1}{(y+1)^{2}+z^{2}+1}+\frac{1}{(z+1)^{2}+x^{2}+1} \leq \frac{1}{2}\left(\frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}\right) C = ( x + 1 ) 2 + y 2 + 1 1 + ( y + 1 ) 2 + z 2 + 1 1 + ( z + 1 ) 2 + x 2 + 1 1 ≤ 2 1 ( 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 )
Mà ta đã biết đẳng thức:
1 1 + x + x y + 1 1 + y + y z + 1 1 + z + z x = 1 \frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}=1 1 + x + x y 1 + 1 + y + yz 1 + 1 + z + z x 1 = 1 Vậy giá trị lớn nhất C là
1 2 \frac{1}{2} 2 1 Đẳng thức xảy ra khi
x = y = z = 1 \mathrm{x}=\mathrm{y}=\mathrm{z}=1 x = y = z = 1 .
C.Bài tập Bài 1. Cho ba số thực dương $a, b, c$ thỏa mãn $a b c=1$. Tìm giá trị nhỏ nhất của biểu thức: P = ( 1 + a ) 2 + b 2 + 5 a b + a + 4 + ( 1 + b ) 2 + c 2 + 5 b c + b + 4 + ( 1 + c ) 2 + a 2 + 5 c a + c + 4 \mathrm{P}=\frac{(1+\mathrm{a})^{2}+\mathrm{b}^{2}+5}{\mathrm{ab}+\mathrm{a}+4}+\frac{(1+\mathrm{b})^{2}+\mathrm{c}^{2}+5}{\mathrm{bc}+\mathrm{b}+4}+\frac{(1+\mathrm{c})^{2}+\mathrm{a}^{2}+5}{\mathrm{ca}+\mathrm{c}+4} P = ab + a + 4 ( 1 + a ) 2 + b 2 + 5 + bc + b + 4 ( 1 + b ) 2 + c 2 + 5 + ca + c + 4 ( 1 + c ) 2 + a 2 + 5 (Trích đề thi lớp 10 Chuyên Quảng Nam năm 2019-2020)
Hướng dẫn giải Ta có:
( 1 + a ) 2 + b 2 + 5 a b + a + 4 = a 2 + b 2 + 2 a + 6 a b + a + 4 ≥ 2 a b + 2 a + 6 a b + a + 4 = 2 ( a b + a + 4 ) − 2 a b + a + 4 = 2 − 2 a b + a + 4 \frac{(1+a)^{2}+b^{2}+5}{ab+a+4}=\frac{a^{2}+b^{2}+2 a+6}{a b+a+4} \geq \frac{2 a b+2 a+6}{a b+a+4}=\frac{2(a b+a+4)-2}{a b+a+4}=2-\frac{2}{a b+a+4} ab + a + 4 ( 1 + a ) 2 + b 2 + 5 = ab + a + 4 a 2 + b 2 + 2 a + 6 ≥ ab + a + 4 2 ab + 2 a + 6 = ab + a + 4 2 ( ab + a + 4 ) − 2 = 2 − ab + a + 4 2
Tương tự:
( 1 + c ) 2 + a 2 + 5 c a + c + 4 ≥ 2 − 2 c a + c + 4 \quad \frac{(1+c)^{2}+a^{2}+5}{c a+c+4} \geq 2-\frac{2}{c a+c+4} c a + c + 4 ( 1 + c ) 2 + a 2 + 5 ≥ 2 − c a + c + 4 2
Do đó:
P ≥ 6 − 2 ( 1 a b + a + 4 + 1 b c + b + 4 + 1 c a + c + 4 ) = 6 − 2 Q \mathrm{P} \geq 6-2\left(\frac{1}{\mathrm{ab}+\mathrm{a}+4}+\frac{1}{\mathrm{bc}+\mathrm{b}+4}+\frac{1}{\mathrm{ca}+\mathrm{c}+4}\right)=6-2 \mathrm{Q} P ≥ 6 − 2 ( ab + a + 4 1 + bc + b + 4 1 + ca + c + 4 1 ) = 6 − 2 Q
Với
x , y x, y x , y dương ta có:
( x − y ) 2 ≥ 0 ⇔ ( x + y ) 2 ≥ 4 x y ⇔ 1 x + y ≤ x + y 4 x y ⇔ 1 x + y ≤ 1 4 ( 1 x + 1 y ) (*) \begin{aligned}(x-y)^{2} \geq 0 &\Leftrightarrow(x+y)^{2} \geq 4 x y\\ &\Leftrightarrow \frac{1}{x+y} \leq \frac{x+y}{4 x y} \\& \Leftrightarrow \frac{1}{x+y} \leq \frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\tag{*}\end{aligned} ( x − y ) 2 ≥ 0 ⇔ ( x + y ) 2 ≥ 4 x y ⇔ x + y 1 ≤ 4 x y x + y ⇔ x + y 1 ≤ 4 1 ( x 1 + y 1 ) ( * )
Dấu "
= = = " xảy ra khi
x = y x=y x = y .
Áp dụng
( ∗ ) \left(^{*}\right) ( ∗ ) ta được:
1 a b + a + 4 = 1 ( a b + a + 1 ) + 3 ≤ 1 4 ( 1 a b + a + 1 + 1 3 ) \frac{1}{a b+a+4}=\frac{1}{(a b+a+1)+3} \leq \frac{1}{4}\left(\frac{1}{ab+a+1}+\frac{1}{3}\right) ab + a + 4 1 = ( ab + a + 1 ) + 3 1 ≤ 4 1 ( ab + a + 1 1 + 3 1 )
Tương tự:
1 b c + b + 4 ≤ 1 4 ( 1 b c + b + 1 + 1 3 ) ; \frac{1}{\mathrm{bc}+\mathrm{b}+4} \leq \frac{1}{4}\left(\frac{1}{\mathrm{bc}+\mathrm{b}+1}+\frac{1}{3}\right) ; bc + b + 4 1 ≤ 4 1 ( bc + b + 1 1 + 3 1 ) ; 1 c a + c + 4 ≤ 1 4 ( 1 c a + c + 1 + 1 3 ) \frac{1}{\mathrm{ca}+\mathrm{c}+4} \leq \frac{1}{4}\left(\frac{1}{\mathrm{ca}+\mathrm{c}+1}+\frac{1}{3}\right) ca + c + 4 1 ≤ 4 1 ( ca + c + 1 1 + 3 1 )
Do đó:
Q ≤ 1 4 ( 1 a b + a + 1 + 1 b c + b + 1 + 1 c a + c + 1 + 1 ) ⇒ 2 Q = 1 2 ( 1 a b + a + 1 + 1 b c + b + 1 + 1 c a + c + 1 + 1 ) ⇒ P ≥ 6 − 1 2 ( 1 a b + a + 1 + 1 b c + b + 1 + 1 c a + c + 1 + 1 ) = 6 − 1 2 ( c a b c + a c + c + a c b c ⋅ a c + a b c + 1 + 1 c a + c + 1 + 1 ) = 6 − 1 2 ( c c a + c + 1 + a c c a + c + 1 + 1 c a + c + 1 + 1 ) = 6 − 1 2 . 2 = 5 \begin{aligned}\mathrm{Q} & \leq\frac{1}{4}\left(\frac{1}{\mathrm{ab}+\mathrm{a}+1}+\frac{1}{\mathrm{bc}+\mathrm{b}+1}+\frac{1}{\mathrm{ca}+\mathrm{c}+1}+1\right) \\\Rightarrow 2\mathrm{Q}&=\frac{1}{2}\left(\frac{1}{\mathrm{ab}+\mathrm{a}+1}+\frac{1}{\mathrm{bc}+\mathrm{b}+1}+\frac{1}{\mathrm{ca}+\mathrm{c}+1}+1\right) \\\Rightarrow \mathrm{P} & \geq 6-\frac{1}{2}\left(\frac{1}{\mathrm{ab}+\mathrm{a}+1}+\frac{1}{\mathrm{bc}+\mathrm{b}+1}+\frac{1}{\mathrm{ca}+\mathrm{c}+1}+1\right) \\& =6-\frac{1}{2}\left(\frac{\mathrm{c}}{\mathrm{abc}+\mathrm{ac}+\mathrm{c}}+\frac{\mathrm{ac}}{\mathrm{bc} \cdot \mathrm{ac}+\mathrm{abc}+1}+\frac{1}{\mathrm{ca}+\mathrm{c}+1}+1\right) \\&=6-\frac{1}{2}\left(\frac{\mathrm{c}}{\mathrm{ca}+\mathrm{c}+1}+\frac{\mathrm{ac}}{\mathrm{ca}+\mathrm{c}+1}+\frac{1}{\mathrm{ca}+\mathrm{c}+1}+1\right) \\& =6-\frac{1}{2} .2 \\& =5\end{aligned} Q ⇒ 2 Q ⇒ P ≤ 4 1 ( ab + a + 1 1 + bc + b + 1 1 + ca + c + 1 1 + 1 ) = 2 1 ( ab + a + 1 1 + bc + b + 1 1 + ca + c + 1 1 + 1 ) ≥ 6 − 2 1 ( ab + a + 1 1 + bc + b + 1 1 + ca + c + 1 1 + 1 ) = 6 − 2 1 ( abc + ac + c c + bc ⋅ ac + abc + 1 ac + ca + c + 1 1 + 1 ) = 6 − 2 1 ( ca + c + 1 c + ca + c + 1 ac + ca + c + 1 1 + 1 ) = 6 − 2 1 .2 = 5
D a ˆ ˊ u "=" xảy ra khi a = b = c = 1 . \text { Dấu "=" xảy ra khi } \mathrm{a}=\mathrm{b}=\mathrm{c}=1 \text {. } D a ˆ ˊ u "=" xảy ra khi a = b = c = 1 .
Vậy giá trị nhỏ nhất của P là 5 .
Bài 2. Cho ba số thực dương a , b , c \mathrm{a}, \mathrm{b}, \mathrm{c} a , b , c thỏa mãn a b c = 1 \mathrm{abc}=1 abc = 1 . Tìm giá trị lớn nhất của biểu thức:
a a + 2 b + b b + 2 c + c c + 2 a \frac{a}{a+2 b}+\frac{b}{b+2 c}+\frac{c}{c+2 a} a + 2 b a + b + 2 c b + c + 2 a c Hướng dẫn giải Vì abc =1 nên
a a + 2 b = a a + 2 a b 2 c = 1 1 + 2 b 2 c ≥ 1 1 + b 2 + b 2 c 2 \frac{a}{a+2 b}=\frac{a}{a+2 a b^{2}c}=\frac{1}{1+2 b^{2} c} \geq \frac{1}{1+b^{2}+b^{2} c^{2}} a + 2 b a = a + 2 a b 2 c a = 1 + 2 b 2 c 1 ≥ 1 + b 2 + b 2 c 2 1
(do áp dụng bất đẳng thức
AM-GM với hai số dương
b 2 \mathrm{b}^{2} b 2 và
b 2 c 2 \mathrm{b}^{2} \mathrm{c}^{2} b 2 c 2 ).
Tương tự:
b b + 2 c ≥ 1 1 + c 2 + c 2 a 2 \frac{b}{b+2 c} \geq \frac{1}{1+c^{2}+c^{2} a^{2}} b + 2 c b ≥ 1 + c 2 + c 2 a 2 1 c c + 2 a ≥ 1 1 + a 2 + a 2 b 2 \frac{c}{c+2 a} \geq \frac{1}{1+a^{2}+a^{2} b^{2}} c + 2 a c ≥ 1 + a 2 + a 2 b 2 1
Do đó:
a a + 2 b + b b + 2 c + c c + 2 a ≥ 1 1 + b 2 + b 2 c 2 + 1 1 + c 2 + c 2 a 2 + 1 1 + a 2 + a 2 b 2 = 1 \begin{aligned}&\frac{a}{a+2 b}+\frac{b}{b+2 c}+\frac{c}{c+2 a}\\&\geq \frac{1}{1+b^{2}+b^{2}c^{2}}+\frac{1}{1+c^{2}+c^{2} a^{2}}+\frac{1}{1+a^{2}+a^{2} b^{2}}\\&=1\end{aligned} a + 2 b a + b + 2 c b + c + 2 a c ≥ 1 + b 2 + b 2 c 2 1 + 1 + c 2 + c 2 a 2 1 + 1 + a 2 + a 2 b 2 1 = 1
Đẳng thức xảy ra khi
a = b = c = 1 \mathrm{a}=\mathrm{b}=\mathrm{c}=1 a = b = c = 1 .
Bài 3*: Cho a , b , c \mathrm{a}, \mathrm{b}, \mathrm{c} a , b , c thực dương thỏa mãn a b c = 1 \mathrm{abc}=1 abc = 1 . Chứng minh rằng:
1 a 4 − a 3 + a b − 2 + 1 b 4 − b 3 + b c + 2 + 1 c 4 + c 3 + a c + 2 ≤ 3 \frac{1}{\sqrt{a^{4}-a^{3}+a b-2}}+\frac{1}{\sqrt{b^{4}-b^{3}+b c+2}}+\frac{1}{\sqrt{c^{4}+c^{3}+a c+2}} \leq \sqrt{3} a 4 − a 3 + ab − 2 1 + b 4 − b 3 + b c + 2 1 + c 4 + c 3 + a c + 2 1 ≤ 3
Xem Thêm Các Chủ đề đang được xem nhiều nhất
Xem Thêm Các Bài Hệ Thống Kiến Thức :
LIÊN HỆ
📬 toancodiem.xinchao@gmail.com
📇169/2 Nguyễn Văn Cừ Phường 2 Q5 TPHCM
Đăng kí Học - Thời Khoá biểu
📞 +84-908-986-786 (Cô Diễm)
Hỗ Trợ Học Viên
📞+84-765-359-411 (anh Quân)