AITA? Số 1: Phân tích và hướng dẫn giải chi tiết: Hình bình hành, trung điểm và giao điểm đường nối, đường chéo
Bài viết cung cấp hướng dẫn chi tiết cách giải bài tập hình bình hành, tập trung vào các khía cạnh quan trọng như tìm trung điểm, giao điểm của các đường nối trong hình học. Bài viết phân tích từng bước một, từ các khái niệm cơ bản đến các kỹ thuật giải nâng cao, giúp học sinh hiểu rõ và áp dụng thành thạo vào các bài toán khác nhau. Với hướng dẫn cụ thể từ Toán Cô Diễm, bạn sẽ có một nền tảng vững chắc để giải quyết các bài tập hình học phức tạp.”
Đây là câu trả lời cho bài toán được bạn Anh d*92 gửi cho Toán Cô Diễm về tính chất của hình bình hành
Yêu cầu

Phân tích giải thiết

Hình Vẽ
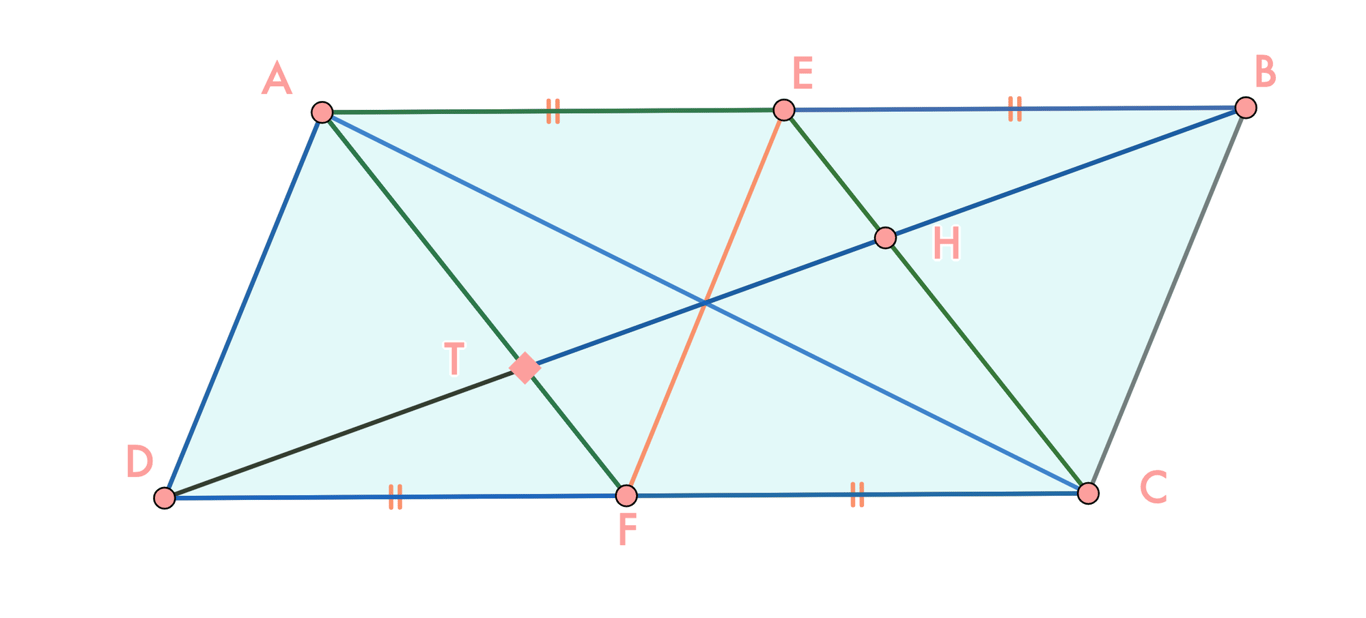
Suy Luận
- Từ giả thiết hình bình hành ta có các đường song song
- Câu 1, cần Chứng minh DT = TH = HB (1), ta quy đổi nó ra thành các mệnh đề tương đương để tìm hướng chứng minh
- (1), "đồng nghĩa" ( tương đương) với T là trung điểm DH, H là trung điểm BT (2) Nếu ta chứng minh được (2) thì bài toán xong.
- Một trong những công cụ chứng minh trung điểm khi có đường song song là định lý
đường thẳng đi qua trung điểm của một cạnh tam giác và song song với cạnh thứ hai, đường thẳng đó cũng sẽ đi qua trung điểm của cạnh thứ ba.
- Một hướng suy nghĩ khác, (1) "đồng nghĩa" với độ dài DT có tỉ lệ . Yêu cầu ban đầu trở thành “nhiệm vụ” chứng minh độ dài hai cạnh trên có tỉ số bằng 1:2. Từ đó ta hướng đến tìm một công cụ để chứng minh tỉ số giữa hai đoạn thẳng khi có các đường song song, là Định Lý Thales (Ta-lét)
- Cùng với suy nghĩ số 5, nếu ta để ý giả thiết cung cấp khá nhiều các trung điểm các đoạn, và điều cần chứng minh trở thành chứng minh tỉ số hai đoạn thẳng là một số, ta nghĩ tới Tính chất của Trọng Tâm Tam Giác
Hướng dẫn giải chi tiết:
Cách 1: Dùng Định Lý Thales
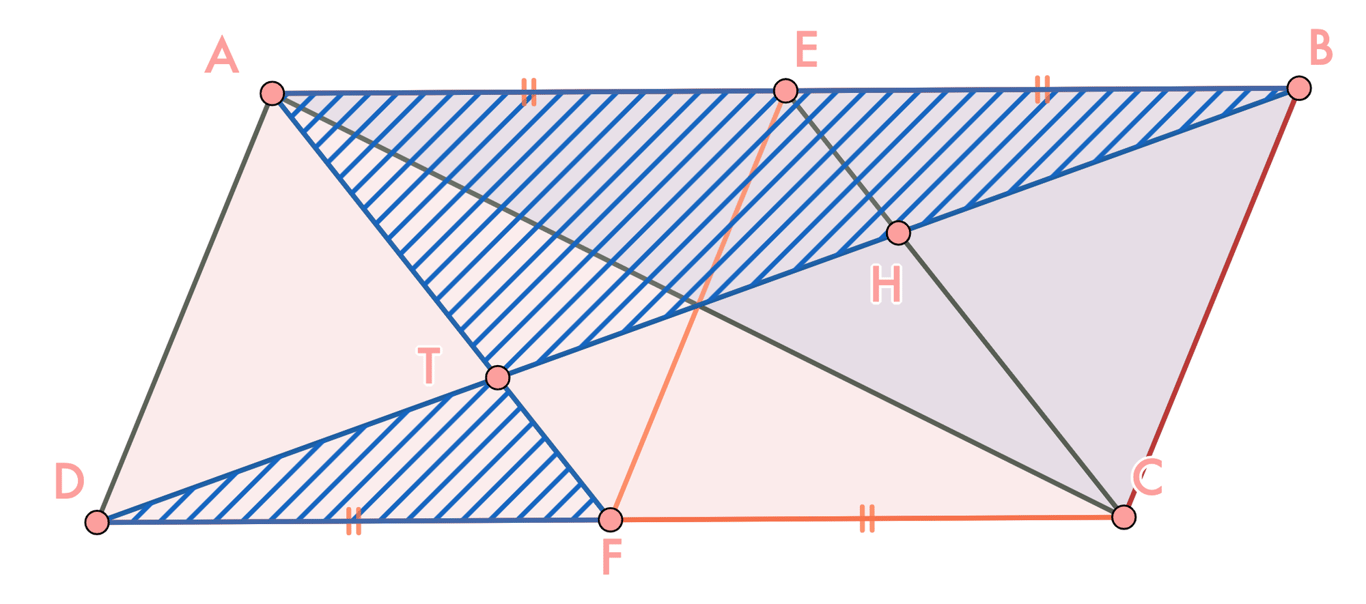
1. Chứng minh

2. Chứng minh rằng các tứ giác AECF, ETFH, ATCH là các hình bình hành
Nhận xét, lần lượt là các đường trung bình của các tam giác (🔆)
- Chứng minh tứ giác ETFH là hình bình hành
- Dấu hiệu 2: Tứ giác có hai cặp cạnh đối bằng nhau.
- Dấu hiệu 1: Tứ giác có hai cặp cạnh đối song song.
- Dấu hiệu 3: Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau.
- Dấu hiệu 4: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
để chứng minh hình bình hành ta dùng một trong các dấu hiệu nhận biết sau

- Chứng minh tứ giác AECF, ATCH là hình bình hành:

Cách 2: Dùng Tính chất Hình Bình Hành
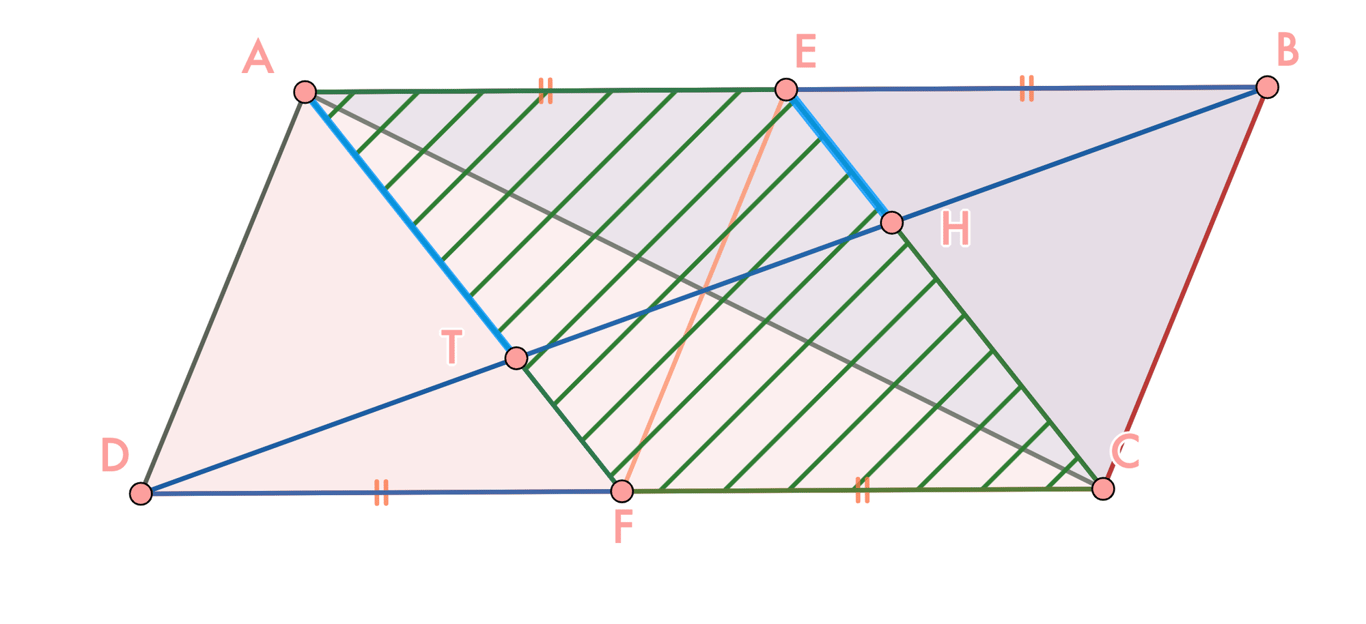

Suy ra và dùng định lý
đường thẳng đi qua trung điểm của một cạnh tam giác và song song với cạnh thứ hai, đường thẳng đó cũng sẽ đi qua trung điểm của cạnh thứ hai.
Cách 3 Dùng tính chất của trọng tâm
Gợi ý :Gọi K là giao điểm AC và BD
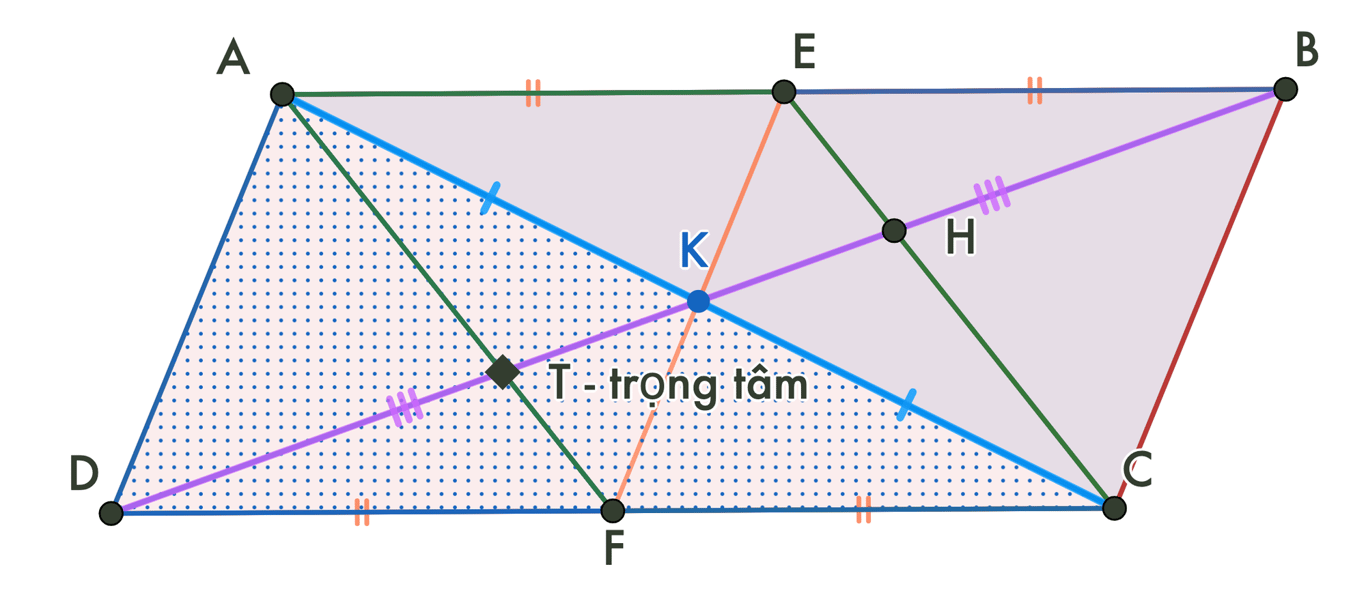
Từ Tính chất của Hình Bình Hành suy ra giao điểm của AC và BD là K là trung điểm của AC và BD.
Trong tam giác ACD hai trung tuyến AF và DK cắt nhau ở T suy ra T là trọng tâm
suy ra . Chứng minh tương tự , mà DK = BK suy ra DPCM
Kết luận
Đối với các bài toán liên quan đến hình bình hành, thì các yếu tố về đường song song, trung điểm, đường trung bình và trực tâm nên được xem xét để suy ra hướng làm bài

Nếu các bạn có đóng góp hoặc ý kiến vui lòng gửi về toancodiem.xinchao@outlook.com
Đừng quên nếu có bài toán cần hỏi thì 👇

Đăng kí Học - Thời Khoá biểu
📞 +84-908-986-786 (Cô Diễm)
Hỗ Trợ Học Viên
📞+84-765-359-411 (anh Quân)