Dưới đây là bài hướng dẫn chi tiết giải Đề luyện tập số 1
Xem lại
Kế hoạch ôn thi HK1
Bài 1: Rút gọn biểu thức căn thức Bài a: Rút gọn:
Bước 1: Rút gọn từng căn thức:
Bước 2: Thay vào biểu thức: Kết quả:
Bài b: Rút gọn:
Bước 1: Áp dụng tính chất căn bậc hai:
Với
, ta có:
Vì
(số dương), nên:
Với
, ta có:
Vì
, nên:
Bước 2: Tính tổng:
Kết quả:
Bài c: Rút gọn:
Đặt:
Bước 1: Khai triển vế phải
Do đó:
So sánh với vế trái:
Bước 2: So sánh các phần
Phần không chứa căn:
Phần chứa căn:
Bước 3: Giải hệ phương trình
Hệ phương trình:
Từ
, suy ra
. Thay vào phương trình thứ nhất:
Nhân với
để khử mẫu:
Đặt
(với
), ta được phương trình:
Bước 4: Giải phương trình bậc hai
Phương trình:
Áp dụng công thức nghiệm:
Nghiệm:
Hoặc
Với
, suy ra:
(do
), khi đó
(do
), khi đó
Ta đặt:
Bước 1: Khai triển vế phải
Do đó:
So sánh với vế trái:
Bước 2: So sánh các phần
Phần không chứa căn:
Phần chứa căn:
Bước 3: Giải hệ phương trình
Hệ phương trình:
Từ
, suy ra
. Thay vào phương trình thứ nhất:
Nhân với
để khử mẫu:
Đặt
(với
), ta được phương trình:
Bước 4: Giải phương trình bậc hai
Phương trình:
Áp dụng công thức nghiệm:
Nghiệm:
hoặc
, suy ra:
(do
), khi đó
(do
), khi đó
Ta chọn được các giá trị nguyên: Với
, chọn
.
Với
, chọn
.
Biểu thức cần tính:
Thay các giá trị đã chọn:
Do đó:
Tính toán:
Kết quả:
Bài d: Rút gọn:
Bước 1: Rút gọn phân thức: Tách mẫu số thứ hai:
Căn thứ ba:
Kết quả:
Bài 2 Giải hệ phương trình:
Bước 1: Rút gọn phương trình thứ nhất Từ phương trình thứ nhất:
Bước 2: Thay vào phương trình thứ hai Thay
vào phương trình thứ hai:
Khai triển:
Bước 3: Tìm
Thay
vào
:
Kết quả: Nghiệm của hệ phương trình:
Bài 3 Xác định và
của đường thẳng
sao cho
song song với
và đi qua điểm
.*
Phân tích bài toán Hai đường thẳng song song có cùng hệ số góc. Do đó:
Thay
và tọa độ điểm
vào phương trình
để tìm
.
Tính toán
Thay
vào phương trình:
Điểm
nằm trên
, do đó:
Kết quả Phương trình đường thẳng
là:
Bài 4 Một máy bay cất cánh với đường bay lên tạo với phương ngang góc
.
a) Tính quãng đường máy bay phải bay để đạt độ cao
(làm tròn 1 chữ số thập phân).
b) Nếu máy bay bay lên với vận tốc
, hỏi thời gian để đạt độ cao đó (làm tròn đến số nguyên).
a) Quãng đường máy bay phải bay Góc
được tạo bởi đường bay lên và phương ngang. Ta có hình tam giác vuông với:
Độ cao là cạnh đối:
Đường bay là cạnh huyền:
Góc
.
Sử dụng hệ thức cạnh góc
Suy ra:
Tra giá trị
:
Đổi sang km:
b) Thời gian để đạt độ cao Vận tốc của máy bay là
. Đổi sang
:
Quãng đường máy bay phải bay:
Thời gian:
Làm tròn:
Kết quả: a) Máy bay phải bay một quãng đường
b) Máy bay mất khoảng
để đạt độ cao
Bài 6 Cho mối quan hệ giữa vận tốc dòng chảy ở bề mặt sông và vận tốc dòng chảy ở đáy sông:
Trong đó:
: vận tốc dòng chảy ở bề mặt sông (km/h),
: vận tốc dòng chảy ở đáy sông (km/h).
Câu a Thay
vào phương trình:
Tính toán:
Bình phương hai vế:
Tính giá trị:
Câu b , tính
Đổi đơn vị
sang km/h:
Thay
vào phương trình:
Tính toán:
Tra giá trị:
Do đó:
Bình phương hai vế:
Tính giá trị:
Kết quả: a) Vận tốc dòng chảy ở đáy sông:
b) Vận tốc dòng chảy ở bề mặt sông:
Bài 7: Tính toán giá xe ô tô
Cách tính thuế thay đổi qua các mốc thời gian. Loại xe có dung tích dưới
áp dụng các mức thuế sau:
Trước ngày
: thuế suất
.
Từ ngày
đến ngày
: thuế suất
.
Từ ngày
trở đi: thuế suất
.
Chú Ba mua một chiếc xe vào ngày
với giá đã tính thuế là
Ký hiệu và công thức tính giá xe Giá xe chưa thuế:
(triệu đồng).
Thuế tiêu thụ đặc biệt: Tỷ lệ phần trăm tương ứng từng giai đoạn.
Giá xe sau thuế:
Giá xe sau thuế = x . (1 + {thuế suất}.
Câu a: Giá xe khi chưa có thuế là bao nhiêu? Giả sử vào ngày 10/10/2017, thuế tiêu thụ đặc biệt là 40%. Ta có phương trình:
(triệu đồng)
Kết luận: Giá xe khi chưa có thuế là 525 triệu đồng.
Câu b: Giá xe (đã tính thuế) nếu mua ngày 16/6/2016?
Vào ngày 16/6/2016, thuế tiêu thụ đặc biệt là 45%.
Giá sau thuế khi đó được tính bằng:
Thay
vào:
Kết luận: Giá xe vào ngày 16/6/2016 là 761.25 triệu đồng.
Câu c: Giá xe (dự kiến) vào ngày 1/1/2018? Dự kiến từ 1/1/2018, thuế tiêu thụ đặc biệt giảm xuống 35%.
Giá sau thuế khi đó được tính bằng:
G s = x ( 1 + 0.35 ) G_s=x(1+0.35) G s = x ( 1 + 0.35 ) Thay
vào:
G s = 525 × 1.35 = 708.75 G_s=525 \times 1.35 = 708.75 G s = 525 × 1.35 = 708.75 Kết luận: Giá xe dự kiến vào ngày 1/1/2018 là 708.75 triệu đồng.
Đáp số: a) Giá xe khi chưa có thuế: 525 triệu đồng.
b) Giá xe ngày 16/6/2016 (đã tính thuế): 761.25 triệu đồng.
c) Giá xe dự kiến ngày 1/1/2018: 708.75 triệu đồng.
Bài 8 Giải bất phương trình
Bất phương trình cần giải là:
Cách1 : Giải bất phương trình bằng xét dấu Bước 1: Quy đồng và đưa về dạng chuẩn
Ta chuyển vế và quy đồng mẫu:
Quy đồng mẫu số:
Khai triển và rút gọn tử số:
Khi đó, bất phương trình trở thành:
Bước 2: Tìm nghiệm và xét dấu
Xét tử số và mẫu số:
Tử số:
.
Mẫu số:
.
Ta xác định các điểm phân chia khoảng nghiệm:
và
.
Lập bảng xét dấu của biểu thức
Cách 2: Giải bất phương trình bằng cách xét hai trường hợp Bất phương trình cần giải:
Phân tích bài toán
Mẫu số
gây ảnh hưởng đến dấu của bất phương trình.
Ta xét hai trường hợp:
và
, đảm bảo rằng mẫu số không bằng 0.
Trường hợp 1: (x < 2)
Khi (x < 2), mẫu số (x - 2 < 0). Nhân cả hai vế với (x - 2) (nhân với số âm nên phải đổi chiều bất phương trình):
Khai triển và rút gọn:
Kết hợp điều kiện (x < 2), ta có:
Trường hợp 2: (x > 2)
Khi (x > 2), mẫu số (x - 2 > 0). Nhân cả hai vế với (x - 2) (nhân với số dương nên giữ nguyên chiều bất phương trình):
Khai triển và rút gọn:
Kết hợp điều kiện (x > 2), ta thấy không tồn tại giá trị (x) thỏa mãn (x \leq -11) và (x > 2).
Do đó, trường hợp này không có nghiệm.
Kết luận Kết hợp cả hai trường hợp, tập nghiệm là:
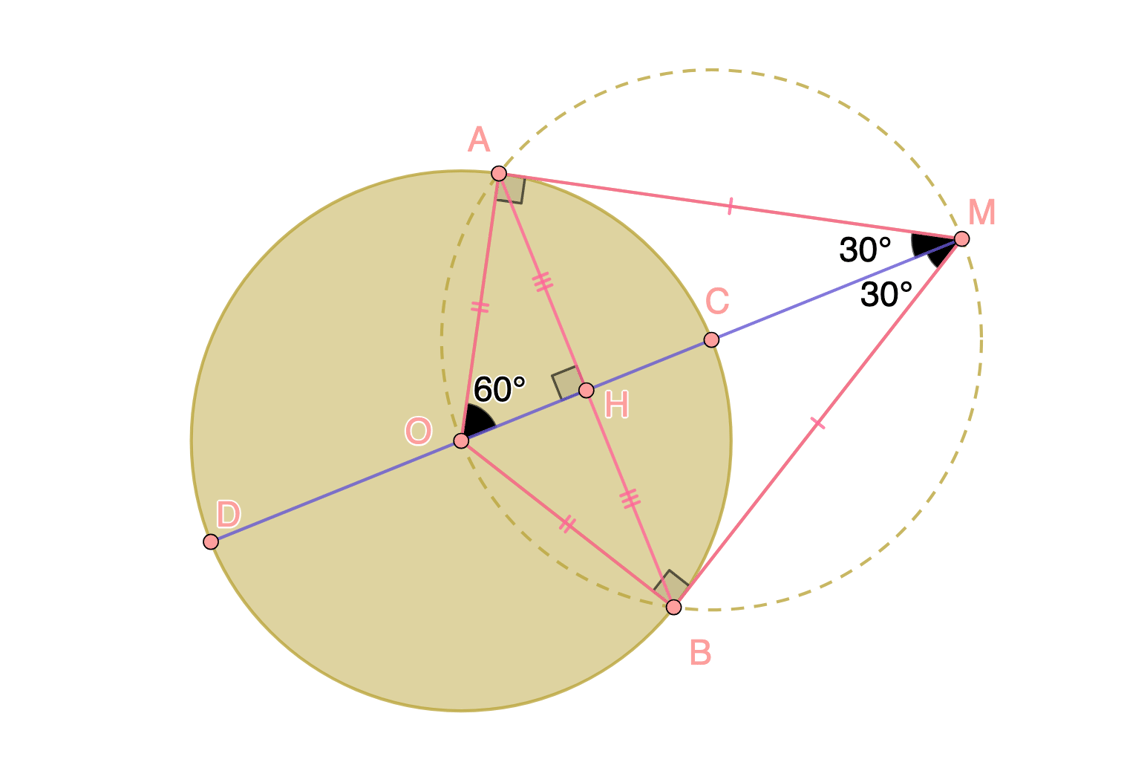
Bài 5 :Hình học Câu a: Chứng minh các điểm cùng thuộc một đường tròn
Xét
và
là tiếp tuyến của
. Do đó, ta có:
Theo tính chất
góc nội tiếp chắn nửa đường tròn , các điểm O, M,A,B cùng thuộc đường tròn đường kính OM với tâm I là trung điểm OM
Kết luận Các điểm
cùng thuộc đường tròn tâm
bán kính
.
Câu b:
Ta có
Suy ra OM là đường trung trực của AB, suy ra OM vuông góc với AB tại H là trung điểm AB
Trong tam giác vuông
, áp dụng định lý Pythagoras:
Tương tự,
Trong tam giác vuông (OMA), ta có:
Tương tự,
.
Do đó:
Mà MA = MB suy ra
, tam giác (ABM) là tam giác đều.
Suy ra
Phần c: Chứng minh bằng cách tính trực tiếp
1. Độ dài (AB): Tam giác (ABM) đều, cạnh (AB) là:
2. Độ dài (AH): (H) là trung điểm của (AB), nên:
3. Độ dài (AC): OC = R = OI ( I là tâm đường tròn (A,B,M,O) mà I, C thuộc đoạn OM
Suy ra C trùng I
Suy ra AC bằng Bán kính của đường tròn (A,B,M,O)
4. Độ dài (HC): Xét tam giác vuông (AHC), áp dụng định lý Pythagoras:
5. Độ dài (MD): 6. Độ dài (CM): 7. Độ dài (DH):
Suy ra
Xem Thêm Các Chủ đề đang được xem nhiều nhất
Xem Thêm Các Bài Hệ Thống Kiến Thức :
LIÊN HỆ
📬 toancodiem.xinchao@gmail.com
📇169/2 Nguyễn Văn Cừ Phường 2 Q5 TPHCM
Đăng kí Học - Thời Khoá biểu
📞 +84-908-986-786 (Cô Diễm)
Hỗ Trợ Học Viên
📞+84-765-359-411 (anh Quân)