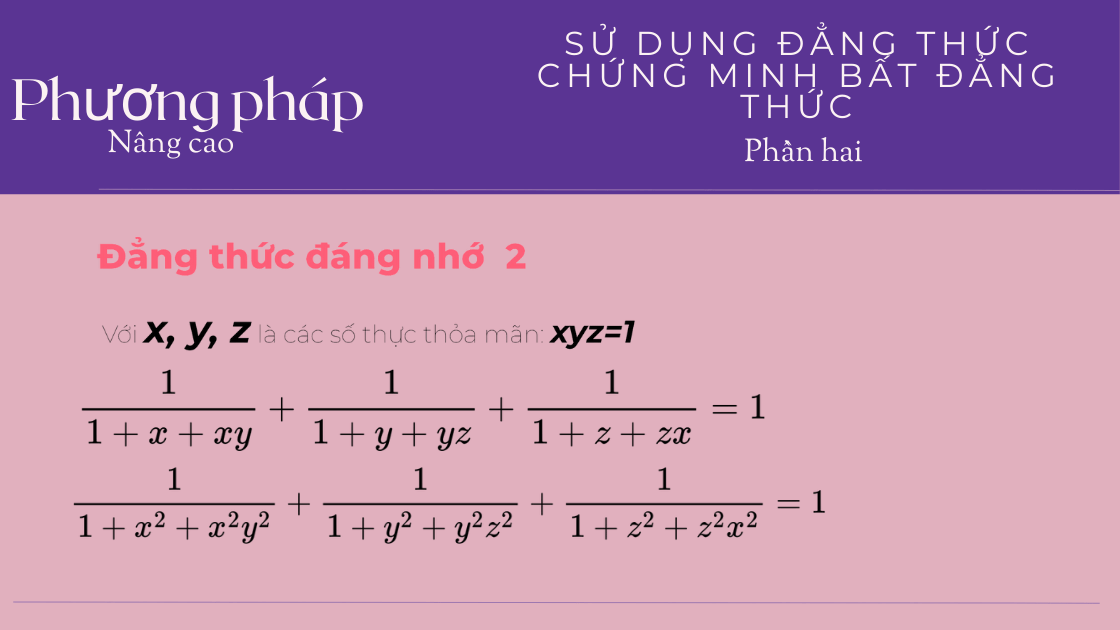
Đề và Hướng Dẫn Giải Chi Tiết – Thi Chính Thức Môn Toán Không Chuyên Phổ Thông Năng Khiếu 2025
Bạn đang ôn thi vào lớp 10 Phổ thông Năng Khiếu? Bài viết cung cấp một đề thi thử môn Toán không chuyên bám sát cấu trúc thật năm 2025, kèm lời giải chi tiết từng câu và phân tích các dạng bài trọng tâm. Đây là tài liệu không thể thiếu cho học sinh, phụ huynh và giáo viên trong hành trình chinh phục PTNK.